|
|
HiddenMarkovModel Class |
Accord.MachineLearningTransformBaseInt32, Int32
Accord.MachineLearningTaggerBaseInt32
Accord.MachineLearningScoreTaggerBaseInt32
Accord.MachineLearningLikelihoodTaggerBaseInt32
Accord.Statistics.Models.MarkovHiddenMarkovModelGeneralDiscreteDistribution, Int32
Accord.Statistics.Models.MarkovHiddenMarkovModel
Namespace: Accord.Statistics.Models.Markov
Assembly: Accord.Statistics (in Accord.Statistics.dll) Version: 3.8.0
[SerializableAttribute] public class HiddenMarkovModel : HiddenMarkovModel<GeneralDiscreteDistribution, int>, IHiddenMarkovModel, ICloneable
The HiddenMarkovModel type exposes the following members.
| Name | Description | |
|---|---|---|
| HiddenMarkovModel(Int32, Int32) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(ITopology, Int32) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(Int32, Int32, Boolean) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(ITopology, Double, Boolean) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(ITopology, Double, Boolean) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(ITopology, Int32, Boolean) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(Double, Double, Double, Boolean) |
Constructs a new Hidden Markov Model.
| |
| HiddenMarkovModel(Double, Double, Double, Boolean) |
Constructs a new Hidden Markov Model.
|
| Name | Description | |
|---|---|---|
| Algorithm |
Gets or sets the algorithm
that should be used to compute solutions to this model's LogLikelihood(T[] input)
evaluation, Decide(T[] input) decoding and LogLikelihoods(T[] input)
posterior problems.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Emissions | Obsolete.
Please use LogEmissions instead.
| |
| LogEmissions |
Gets the log-emission matrix log(B) for this model.
| |
| LogInitial |
Gets the log-initial probabilities log(pi) for this model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogTransitions |
Gets the log-transition matrix log(A) for this model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| NumberOfClasses |
Gets the number of classes expected and recognized by the classifier.
(Inherited from TaggerBaseTInput.) | |
| NumberOfInputs |
Gets the number of inputs accepted by the model.
(Inherited from TransformBaseTInput, TOutput.) | |
| NumberOfOutputs |
Gets the number of outputs generated by the model.
(Inherited from TransformBaseTInput, TOutput.) | |
| NumberOfStates |
Gets the number of states of this model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| NumberOfSymbols |
Gets the number of symbols in this model's alphabet.
| |
| Probabilities | Obsolete.
Please use LogInitial instead.
| |
| States | Obsolete.
Gets the number of states of this model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Symbols | Obsolete.
Please use NumberOfSymbols instead.
| |
| Tag |
Gets or sets a user-defined tag associated with this model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Transitions | Obsolete.
Please use LogTransitions instead.
|
| Name | Description | |
|---|---|---|
| Clone |
Creates a new object that is a copy of the current instance.
(Overrides HiddenMarkovModelTDistribution, TObservationClone.) | |
| CreateDiscrete(Int32, Int32) |
Creates a discrete hidden Markov model using the generic interface.
| |
| CreateDiscrete(ITopology, Int32) |
Creates a discrete hidden Markov model using the generic interface.
| |
| CreateDiscrete(Int32, Int32, Boolean) |
Creates a discrete hidden Markov model using the generic interface.
| |
| CreateDiscrete(ITopology, Int32, Boolean) |
Creates a discrete hidden Markov model using the generic interface.
| |
| CreateDiscrete(Double, Double, Double, Boolean) |
Creates a discrete hidden Markov model using the generic interface.
| |
| CreateGeneric(Int32, Int32) | Obsolete.
Constructs a new Hidden Markov Model with discrete state probabilities.
| |
| CreateGeneric(ITopology, Int32) | Obsolete.
Constructs a new Hidden Markov Model with discrete state probabilities.
| |
| CreateGeneric(Int32, Int32, Boolean) | Obsolete.
Constructs a new Hidden Markov Model with discrete state probabilities.
| |
| CreateGeneric(ITopology, Int32, Boolean) | Obsolete.
Constructs a new Hidden Markov Model with discrete state probabilities.
| |
| CreateGeneric(Double, Double, Double, Boolean) | Obsolete.
Constructs a new discrete-density Hidden Markov Model.
| |
| Decide(TInput) |
Computes class-label decisions for the given input.
(Inherited from TaggerBaseTInput.) | |
| Decide(TInput) |
Computes class-label decisions for the given input.
(Inherited from TaggerBaseTInput.) | |
| Decide(TObservation, Int32) |
Computes class-label decisions for the given input.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Decide(TObservation, Int32) |
Computes class-label decisions for the given input.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Decode(TObservation) | Obsolete.
Calculates the most likely sequence of hidden states
that produced the given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Decode(TObservation, Double) | Obsolete.
Calculates the most likely sequence of hidden states
that produced the given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Evaluate(TObservation) | Obsolete.
Calculates the likelihood that this model has generated the given sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Evaluate(TObservation, Int32) | Obsolete.
Calculates the log-likelihood that this model has generated the
given observation sequence along the given state path.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| Generate(Int32) |
Generates a random vector of observations from the model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Generate(Int32, Int32, Double) |
Generates a random vector of observations from the model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| GetHashCode | Serves as the default hash function. (Inherited from Object.) | |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| Load(Stream) | Obsolete.
Loads a hidden Markov model from a stream.
| |
| Load(String) | Obsolete.
Loads a hidden Markov model from a file.
| |
| LoadTDistribution(Stream) | Obsolete.
Loads a hidden Markov model from a stream.
| |
| LoadTDistribution(String) | Obsolete.
Loads a hidden Markov model from a file.
| |
| LogLikelihood(TInput) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihood(TInput) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihood(TInput, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihood(TInput, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihood(TObservation, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger along
the given path of hidden states.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihood(TObservation, Double) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihood(TObservation, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger along
the given path of hidden states.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihood(TObservation, Int32, Double) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger along
the given path of hidden states.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihood(TObservation, Int32, Double) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihoods(TInput) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TInput) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TInput, Int32) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TInput, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TInput, Int32) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TObservation, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| LogLikelihoods(TInput, Int32, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| LogLikelihoods(TObservation, Int32, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| Posterior(TObservation) | Obsolete.
Calculates the probability of each hidden state for each
observation in the observation vector.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Posterior(TObservation, Int32) | Obsolete.
Calculates the probability of each hidden state for each observation
in the observation vector, and uses those probabilities to decode the
most likely sequence of states for each observation in the sequence
using the posterior decoding method. See remarks for details.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Predict(TObservation) |
Predicts the next observation occurring after a given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Predict(Int32, Double) |
Predicts the next observation occurring after a given observation sequence.
| |
| Predict(Int32, Int32) |
Predicts next observations occurring after a given observation sequence.
(Overrides HiddenMarkovModelTDistribution, TObservationPredict(TObservation, Int32).) | |
| Predict(TObservation, Double) |
Predicts the next observation occurring after a given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Predict(Int32, Int32, Double) |
Predicts next observations occurring after a given observation sequence.
| |
| Predict(TObservation, Int32, Double) |
Predicts the next observations occurring after a given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Predict(Int32, Int32, Double, Double) |
Predicts the next observations occurring after a given observation sequence.
| |
| PredictTMultivariate(TObservation, Double, MultivariateMixtureTMultivariate) |
Predicts the next observation occurring after a given observation sequence.
(Inherited from HiddenMarkovModelTDistribution, TObservation.) | |
| Probabilities(TInput) |
Predicts a the probabilities for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Double) |
Predicts a the probabilities for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Int32) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Int32) |
Predicts a the probabilities for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Int32, Double) |
Predicts a the log-likelihood for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probabilities(TInput, Int32, Double) |
Predicts a the probabilities for each of the observations in
the sequence vector assuming each of the possible states in the
tagger model.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput, Double) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput, Int32) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Probability(TInput, Int32, Double) |
Predicts a the probability that the sequence vector
has been generated by this log-likelihood tagger.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Save(Stream) | Obsolete.
Saves the hidden Markov model to a stream.
| |
| Save(String) | Obsolete.
Saves the hidden Markov model to a stream.
| |
| Scores(TInput) |
Computes numerical scores measuring the association between
each of the given sequence vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| Scores(TInput) |
Computes numerical scores measuring the association between
each of the given sequences vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| Scores(TInput, Double) |
Computes numerical scores measuring the association between
each of the given sequences vectors and each
possible class.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Scores(TInput, Double) |
Computes numerical scores measuring the association between
each of the given sequence vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| Scores(TInput, Int32) |
Computes numerical scores measuring the association between
each of the given sequence vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| Scores(TInput, Int32) |
Computes numerical scores measuring the association between
each of the given sequences vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| Scores(TInput, Int32, Double) |
Computes numerical scores measuring the association between
each of the given sequences vectors and each
possible class.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Scores(TInput, Int32, Double) |
Computes numerical scores measuring the association between
each of the given sequence vectors and each
possible class.
(Inherited from ScoreTaggerBaseTInput.) | |
| ToContinuousModel | Obsolete.
Converts this Discrete density Hidden Markov Model
into a arbitrary density model.
| |
| ToGenericModel |
Converts this Discrete density Hidden Markov Model
into a arbitrary density model.
| |
| ToString | Returns a string that represents the current object. (Inherited from Object.) | |
| Transform(TInput) |
Applies the transformation to an input, producing an associated output.
(Inherited from TaggerBaseTInput.) | |
| Transform(TInput) |
Applies the transformation to a set of input vectors,
producing an associated set of output vectors.
(Inherited from TransformBaseTInput, TOutput.) | |
| Transform(TInput, Double) |
Applies the transformation to an input, producing an associated output.
(Inherited from LikelihoodTaggerBaseTInput.) | |
| Transform(TInput, TOutput) |
Applies the transformation to an input, producing an associated output.
(Inherited from TransformBaseTInput, TOutput.) |
| Name | Description | |
|---|---|---|
| (HiddenMarkovModel to HiddenMarkovModelGeneralDiscreteDistribution) |
Converts this Discrete density Hidden Markov Model
to a Continuous density model.
|
| Name | Description | |
|---|---|---|
| HasMethod |
Checks whether an object implements a method with the given name.
(Defined by ExtensionMethods.) | |
| IsEqual |
Compares two objects for equality, performing an elementwise
comparison if the elements are vectors or matrices.
(Defined by Matrix.) | |
| To(Type) | Overloaded.
Converts an object into another type, irrespective of whether
the conversion can be done at compile time or not. This can be
used to convert generic types to numeric types during runtime.
(Defined by ExtensionMethods.) | |
| ToT | Overloaded.
Converts an object into another type, irrespective of whether
the conversion can be done at compile time or not. This can be
used to convert generic types to numeric types during runtime.
(Defined by ExtensionMethods.) |
Hidden Markov Models (HMM) are stochastic methods to model temporal and sequence data. They are especially known for their application in temporal pattern recognition such as speech, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics.
This page refers to the discrete-density version of the model. For arbitrary density (probability distribution) definitions, please see HiddenMarkovModelTDistribution.
Dynamical systems of discrete nature assumed to be governed by a Markov chain emits a sequence of observable outputs. Under the Markov assumption, it is also assumed that the latest output depends only on the current state of the system. Such states are often not known from the observer when only the output values are observable.
Assuming the Markov probability, the probability of any sequence of observations occurring when following a given sequence of states can be stated as
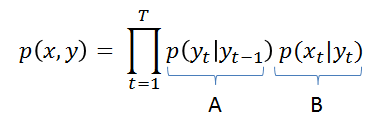
in which the probabilities p(yt|yt-1) can be read as the probability of being currently in state yt given we just were in the state yt-1 at the previous instant t-1, and the probability p(xt|yt) can be understood as the probability of observing xt at instant t given we are currently in the state yt. To compute those probabilities, we simple use two matrices A and B. The matrix A is the matrix of state probabilities: it gives the probabilities p(yt|yt-1) of jumping from one state to the other, and the matrix B is the matrix of observation probabilities, which gives the distribution density p(xt|yt) associated a given state yt. In the discrete case, B is really a matrix. In the continuous case, B is a vector of probability distributions. The overall model definition can then be stated by the tuple
![]()
in which n is an integer representing the total number of states in the system, A is a matrix of transition probabilities, B is either a matrix of observation probabilities (in the discrete case) or a vector of probability distributions (in the general case) and p is a vector of initial state probabilities determining the probability of starting in each of the possible states in the model.
Hidden Markov Models attempt to model such systems and allow, among other things,
- To infer the most likely sequence of states that produced a given output sequence,
- Infer which will be the most likely next state (and thus predicting the next output),
- Calculate the probability that a given sequence of outputs originated from the system (allowing the use of hidden Markov models for sequence classification).
The “hidden” in Hidden Markov Models comes from the fact that the observer does not know in which state the system may be in, but has only a probabilistic insight on where it should be.
To learn a Markov model, you can find a list of both supervised and unsupervised learning algorithms in the Accord.Statistics.Models.Markov.Learning namespace.
References:
- Wikipedia contributors. "Linear regression." Wikipedia, the Free Encyclopedia. Available at: http://en.wikipedia.org/wiki/Hidden_Markov_model
- Nikolai Shokhirev, Hidden Markov Models. Personal website. Available at: http://www.shokhirev.com/nikolai/abc/alg/hmm/hmm.html
- X. Huang, A. Acero, H. Hon. "Spoken Language Processing." pp 396-397. Prentice Hall, 2001.
- Dawei Shen. Some mathematics for HMMs, 2008. Available at: http://courses.media.mit.edu/2010fall/mas622j/ProblemSets/ps4/tutorial.pdf
The example below reproduces the same example given in the Wikipedia entry for the Viterbi algorithm (http://en.wikipedia.org/wiki/Viterbi_algorithm). In this example, the model's parameters are initialized manually. However, it is possible to learn those automatically using BaumWelchLearning.
// In this example, we will reproduce the example on the Viterbi algorithm // available on Wikipedia: http://en.wikipedia.org/wiki/Viterbi_algorithm // Create the transition matrix A double[,] transition = { { 0.7, 0.3 }, { 0.4, 0.6 } }; // Create the emission matrix B double[,] emission = { { 0.1, 0.4, 0.5 }, { 0.6, 0.3, 0.1 } }; // Create the initial probabilities pi double[] initial = { 0.6, 0.4 }; // Create a new hidden Markov model var hmm = new HiddenMarkovModel(transition, emission, initial); // After that, one could, for example, query the probability // of a sequence occurring. We will consider the sequence int[] sequence = new int[] { 0, 1, 2 }; // And now we will evaluate its likelihood double logLikelihood = hmm.LogLikelihood(sequence); // At this point, the log-likelihood of the sequence // occurring within the model is -3.3928721329161653. // We can also get the Viterbi path of the sequence int[] path = hmm.Decode(sequence); // And the likelihood along the Viterbi path is double viterbi; hmm.Decode(sequence, out viterbi); // At this point, the state path will be 1-0-0 and the // log-likelihood will be -4.3095199438871337
If you would like to learn the a hidden Markov model straight from a dataset, you can use:
// We will create a Hidden Markov Model to detect // whether a given sequence starts with a zero. int[][] sequences = new int[][] { new int[] { 0,1,1,1,1,0,1,1,1,1 }, new int[] { 0,1,1,1,0,1,1,1,1,1 }, new int[] { 0,1,1,1,1,1,1,1,1,1 }, new int[] { 0,1,1,1,1,1 }, new int[] { 0,1,1,1,1,1,1 }, new int[] { 0,1,1,1,1,1,1,1,1,1 }, new int[] { 0,1,1,1,1,1,1,1,1,1 }, }; // Create the learning algorithm var teacher = new BaumWelchLearning() { Topology = new Ergodic(3), // Create a new Hidden Markov Model with 3 states for NumberOfSymbols = 2, // an output alphabet of two characters (zero and one) Tolerance = 0.0001, // train until log-likelihood changes less than 0.0001 Iterations = 0 // and use as many iterations as needed }; // Estimate the model var hmm = teacher.Learn(sequences); // Now we can calculate the probability that the given // sequences originated from the model. We can compute // those probabilities using the Viterbi algorithm: double vl1; hmm.Decode(new int[] { 0, 1 }, out vl1); // -0.69317855 double vl2; hmm.Decode(new int[] { 0, 1, 1, 1 }, out vl2); // -2.16644878 // Sequences which do not start with zero have much lesser probability. double vl3; hmm.Decode(new int[] { 1, 1 }, out vl3); // -11.3580034 double vl4; hmm.Decode(new int[] { 1, 0, 0, 0 }, out vl4); // -38.6759130 // Sequences which contains few errors have higher probability // than the ones which do not start with zero. This shows some // of the temporal elasticity and error tolerance of the HMMs. double vl5; hmm.Decode(new int[] { 0, 1, 0, 1, 1, 1, 1, 1, 1 }, out vl5); // -8.22665 double vl6; hmm.Decode(new int[] { 0, 1, 1, 1, 1, 1, 1, 0, 1 }, out vl6); // -8.22665 // Additionally, we can also compute the probability // of those sequences using the forward algorithm: double fl1 = hmm.LogLikelihood(new int[] { 0, 1 }); // -0.000031369 double fl2 = hmm.LogLikelihood(new int[] { 0, 1, 1, 1 }); // -0.087005121 // Sequences which do not start with zero have much lesser probability. double fl3 = hmm.LogLikelihood(new int[] { 1, 1 }); // -10.66485629 double fl4 = hmm.LogLikelihood(new int[] { 1, 0, 0, 0 }); // -36.61788687 // Sequences which contains few errors have higher probability // than the ones which do not start with zero. This shows some // of the temporal elasticity and error tolerance of the HMMs. double fl5 = hmm.LogLikelihood(new int[] { 0, 1, 0, 1, 1, 1, 1, 1, 1 }); // -3.3744416 double fl6 = hmm.LogLikelihood(new int[] { 0, 1, 1, 1, 1, 1, 1, 0, 1 }); // -3.3744416
Hidden Markov Models are generative models, and as such, can be used to generate new samples following the structure that they have learned from the data
Accord.Math.Random.Generator.Seed = 42; // Let's say we have the following set of sequences string[][] phrases = { new[] { "those", "are", "sample", "words", "from", "a", "dictionary" }, new[] { "those", "are", "sample", "words" }, new[] { "sample", "words", "are", "words" }, new[] { "those", "words" }, new[] { "those", "are", "words" }, new[] { "words", "from", "a", "dictionary" }, new[] { "those", "are", "words", "from", "a", "dictionary" } }; // Let's begin by transforming them to sequence of // integer labels using a codification codebook: var codebook = new Codification("Words", phrases); // Now we can create the training data for the models: int[][] sequence = codebook.Translate("Words", phrases); // To create the models, we will specify a forward topology, // as the sequences have definite start and ending points. // var topology = new Forward(states: 4); int symbols = codebook["Words"].Symbols; // We have 7 different words // Create the hidden Markov model var hmm = new HiddenMarkovModel(topology, symbols); // Create the learning algorithm var teacher = new BaumWelchLearning(hmm); // Teach the model teacher.Learn(sequence); // Now, we can ask the model to generate new samples // from the word distributions it has just learned: // int[] sample = hmm.Generate(3); // And the result will be: "those", "are", "words". string[] result = codebook.Translate("Words", sample);
Hidden Markov Models can also be used to predict the next observation in a sequence. This can be done by inspecting the forward matrix of probabilities for the sequence and inspecting all states and possible symbols to find which state-observation combination would be the most likely after the current ones. This limits the applicability of this model to only very short-term predictions (i.e. most likely, only the most immediate next observation).
// We will try to create a Hidden Markov Model which // can recognize (and predict) the following sequences: int[][] sequences = { new[] { 1, 3, 5, 7, 9, 11, 13 }, new[] { 1, 3, 5, 7, 9, 11 }, new[] { 1, 3, 5, 7, 9, 11, 13 }, new[] { 1, 3, 3, 7, 7, 9, 11, 11, 13, 13 }, new[] { 1, 3, 7, 9, 11, 13 }, }; // Create a Baum-Welch HMM algorithm: var teacher = new BaumWelchLearning() { // Let's creates a left-to-right (forward) // Hidden Markov Model with 7 hidden states Topology = new Forward(7), // We'll try to fit the model to the data until the difference in // the average log-likelihood changes only by as little as 0.0001 Tolerance = 0.0001, Iterations = 0 // do not impose a limit on the number of iterations }; // Use the algorithm to learn a new Markov model: HiddenMarkovModel hmm = teacher.Learn(sequences); // Now, we will try to predict the next 1 observation in a base symbol sequence int[] prediction = hmm.Predict(observations: new[] { 1, 3, 5, 7, 9 }, next: 1); // At this point, prediction should be int[] { 11 } int nextSymbol = prediction[0]; // should be 11. // We can try to predict further, but this might not work very // well due the Markov assumption between the transition states: int[] nextSymbols = hmm.Predict(observations: new[] { 1, 3, 5, 7 }, next: 2); // At this point, nextSymbols should be int[] { 9, 11 } int nextSymbol1 = nextSymbols[0]; // 9 int nextSymbol2 = nextSymbols[1]; // 11
For more examples on how to learn discrete models, please see the BaumWelchLearning documentation page. For continuous models (models that can model more than just integer labels), please see BaumWelchLearningTDistribution, TObservation.