|
|
MeanShift Class |
Namespace: Accord.MachineLearning
Assembly: Accord.MachineLearning (in Accord.MachineLearning.dll) Version: 3.8.0
[SerializableAttribute] public class MeanShift : ParallelLearningBase, IUnsupervisedLearning<MeanShiftClusterCollection, double[], int>, IClusteringAlgorithm<double[]>, IUnsupervisedLearning<IClusterCollection<double[]>, double[], int>
The MeanShift type exposes the following members.
| Name | Description | |
|---|---|---|
| MeanShift |
Creates a new MeanShift algorithm.
| |
| MeanShift(IRadiallySymmetricKernel, Double) |
Creates a new MeanShift algorithm.
| |
| MeanShift(Int32, IRadiallySymmetricKernel, Double) | Obsolete.
Creates a new MeanShift algorithm.
|
| Name | Description | |
|---|---|---|
| Bandwidth |
Gets or sets the bandwidth (radius, or smoothness)
parameter to be used in the mean-shift algorithm.
| |
| Clusters |
Gets the clusters found by Mean Shift.
| |
| ComputeLabels |
Gets or sets whether cluster labels should be computed
at the end of the learning iteration. Setting to False
might save a few computations in case they are not necessary.
| |
| ComputeProportions |
Gets or sets whether cluster proportions should be computed
at the end of the learning iteration. Setting to False
might save a few computations in case they are not necessary.
| |
| Dimension |
Gets the dimension of the samples being
modeled by this clustering algorithm.
| |
| Distance |
Gets or sets the IMetricT used to
compute distances between points in the clustering.
| |
| Kernel |
Gets or sets the density kernel to be used in the algorithm.
Default is to use the UniformKernel.
| |
| Maximum |
Gets or sets the maximum number of neighbors which should be
used to determine the direction of the mean-shift during the
computations. Default is zero (unlimited number of neighbors).
| |
| MaxIterations |
Gets or sets the maximum number of iterations to
be performed by the method. If set to zero, no
iteration limit will be imposed. Default is 0.
| |
| ParallelOptions |
Gets or sets the parallelization options for this algorithm.
(Inherited from ParallelLearningBase.) | |
| Token |
Gets or sets a cancellation token that can be used
to cancel the algorithm while it is running.
(Inherited from ParallelLearningBase.) | |
| Tolerance |
Gets or sets the relative convergence threshold
for stopping the algorithm. Default is 1e-3.
| |
| UseAgglomeration |
Gets or sets whether to use the agglomeration shortcut,
meaning the algorithm will stop early when it detects that
a sample is going to follow the same path as another sample
when running in parallel.
| |
| UseParallelProcessing | Obsolete.
Gets or sets whether the algorithm can use parallel
processing to speedup computations. Enabling parallel
processing can, however, result in different results
at each run.
| |
| UseSeeding |
Gets or sets whether to use seeding to initialize the algorithm.
With seeding, new points will be sampled from an uniform grid in
the range of the input points to be used as seeds. Otherwise, the
input points themselves will be used as the initial centroids for
the algorithm.
|
| Name | Description | |
|---|---|---|
| Compute(Double) | Obsolete.
Divides the input data into clusters.
| |
| Compute(Double, Int32) | Obsolete.
Divides the input data into clusters.
| |
| Equals | Determines whether the specified object is equal to the current object. (Inherited from Object.) | |
| Finalize | Allows an object to try to free resources and perform other cleanup operations before it is reclaimed by garbage collection. (Inherited from Object.) | |
| GetHashCode | Serves as the default hash function. (Inherited from Object.) | |
| GetType | Gets the Type of the current instance. (Inherited from Object.) | |
| Learn(Double, Double) |
Learns a model that can map the given inputs to the desired outputs.
| |
| Learn(Double, Int32) |
Learns a model that can map the given inputs to the desired outputs.
| |
| MemberwiseClone | Creates a shallow copy of the current Object. (Inherited from Object.) | |
| ToString | Returns a string that represents the current object. (Inherited from Object.) |
| Name | Description | |
|---|---|---|
| HasMethod |
Checks whether an object implements a method with the given name.
(Defined by ExtensionMethods.) | |
| IsEqual |
Compares two objects for equality, performing an elementwise
comparison if the elements are vectors or matrices.
(Defined by Matrix.) | |
| To(Type) | Overloaded.
Converts an object into another type, irrespective of whether
the conversion can be done at compile time or not. This can be
used to convert generic types to numeric types during runtime.
(Defined by ExtensionMethods.) | |
| ToT | Overloaded.
Converts an object into another type, irrespective of whether
the conversion can be done at compile time or not. This can be
used to convert generic types to numeric types during runtime.
(Defined by ExtensionMethods.) |
Mean shift is a non-parametric feature-space analysis technique originally presented in 1975 by Fukunaga and Hostetler. It is a procedure for locating the maxima of a density function given discrete data sampled from that function. The method iteratively seeks the location of the modes of the distribution using local updates.
As it is, the method would be intractable; however, some clever optimizations such as the use of appropriate data structures and seeding strategies as shown in Lee (2011) and Carreira-Perpinan (2006) can improve its computational speed.
References:
- Wikipedia, The Free Encyclopedia. Mean-shift. Available on: http://en.wikipedia.org/wiki/Mean-shift
- Comaniciu, Dorin, and Peter Meer. "Mean shift: A robust approach toward feature space analysis." Pattern Analysis and Machine Intelligence, IEEE Transactions on 24.5 (2002): 603-619. Available at: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1000236
- Conrad Lee. Scalable mean-shift clustering in a few lines of python. The Sociograph blog, 2011. Available at: http://sociograph.blogspot.com.br/2011/11/scalable-mean-shift-clustering-in-few.html
- Carreira-Perpinan, Miguel A. "Acceleration strategies for Gaussian mean-shift image segmentation." Computer Vision and Pattern Recognition, 2006 IEEE Computer Society Conference on. Vol. 1. IEEE, 2006. Available at: http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=1640881
The following example demonstrates how to use the Mean Shift algorithm with a uniform kernel to solve a clustering task:
// Use a fixed seed for reproducibility Accord.Math.Random.Generator.Seed = 0; // Declare some data to be clustered double[][] input = { new double[] { -5, -2, -4 }, new double[] { -5, -5, -6 }, new double[] { 2, 1, 1 }, new double[] { 1, 1, 2 }, new double[] { 1, 2, 2 }, new double[] { 3, 1, 2 }, new double[] { 11, 5, 4 }, new double[] { 15, 5, 6 }, new double[] { 10, 5, 6 }, }; // Create a new Mean-Shift algorithm for 3 dimensional samples MeanShift meanShift = new MeanShift() { // Use a uniform kernel density Kernel = new UniformKernel(), Bandwidth = 2.0 }; // Learn a data partitioning using the Mean Shift algorithm MeanShiftClusterCollection clustering = meanShift.Learn(input); // Predict group labels for each point int[] labels = clustering.Decide(input); // As a result, the first two observations should belong to the // same cluster (thus having the same label). The same should // happen to the next four observations and to the last three.
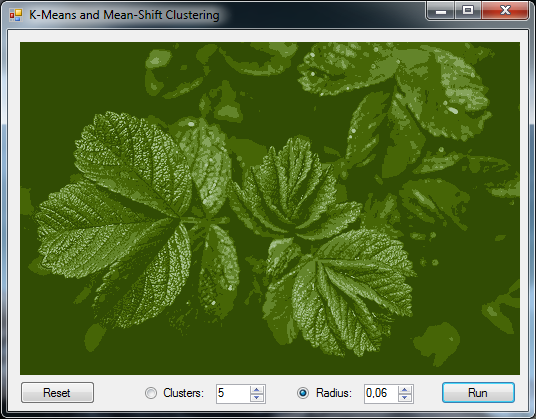
The following example demonstrates how to use the Mean Shift algorithm for color clustering. It is the same code which can be found in the color clustering sample application.
// Load a test image (shown in a picture box below) var sampleImages = new TestImages(path: basePath); Bitmap image = sampleImages.GetImage("airplane.png"); // ImageBox.Show("Original", image).Hold(); // Create converters to convert between Bitmap images and double[] arrays var imageToArray = new ImageToArray(min: -1, max: +1); var arrayToImage = new ArrayToImage(image.Width, image.Height, min: -1, max: +1); // Transform the image into an array of pixel values double[][] pixels; imageToArray.Convert(image, out pixels); // Create a MeanShift algorithm using given bandwidth // and a Gaussian density kernel as kernel function. MeanShift meanShift = new MeanShift() { Kernel = new GaussianKernel(3), Bandwidth = 0.06, // We will compute the mean-shift algorithm until the means // change less than 0.05 between two iterations of the algorithm Tolerance = 0.05, MaxIterations = 10 }; // Learn the clusters from the data var clusters = meanShift.Learn(pixels); // Use clusters to decide class labels int[] labels = clusters.Decide(pixels); // Replace every pixel with its corresponding centroid double[][] replaced = pixels.Apply((x, i) => clusters.Modes[labels[i]]); // Retrieve the resulting image (shown in a picture box) Bitmap result; arrayToImage.Convert(replaced, out result); // ImageBox.Show("Mean-Shift clustering", result).Hold();
The original image is shown below:
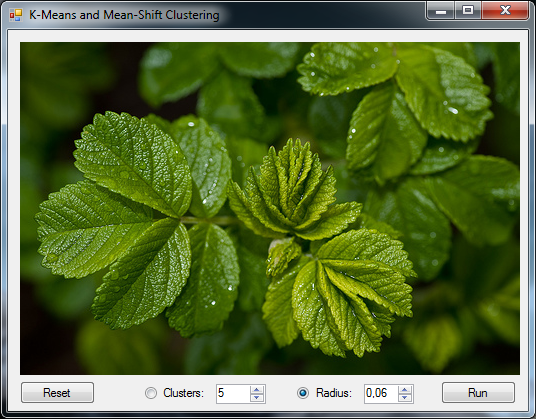
The resulting image will be: